Table of Contents
Batch simulations
The time it takes to run a simulation is often exponential to the number states (compartments x materials).
Running simulations in batches mean that a model is divided into smaller independent parts which are solved in sequence.
There are two types of batches: those that are completely independent, and those where the second batch depends on the results from the first (but not vice versa).
The example model below consists of four compartments and two materials:
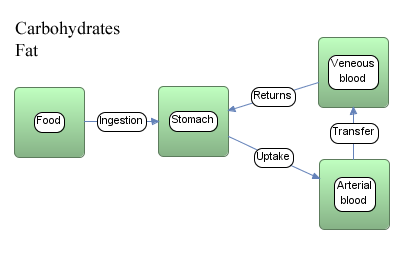The total number of states are 8:
| State |
|---|
| Food[Carbohydrates] |
| Stomach[Carbohydrates] |
| Arterial[Carbohydrates] |
| Veneous[Carbohydrates] |
| Food[Fat] |
| Stomach[Fat] |
| Arterial[Fat] |
| Veneous[Fat] |
Independent batches
| Note | Nuclide decay chains will cause dependencies between material, so that a batch must include all nuclides of the chain. |
If we assume that there is no (mathematical) dependence between the two materials in the model above, the model could be seen as two seperate models: one for Carbohydrates and one for Fat. One can therefore safely solve the equations first for Carbohydrates and then for Fat, which would reduce the number of states per simulation to 4.
The option to run independent batches has been available since Ecolego 5.
| Batch 1 | Batch 2 |
|---|---|
| Food[Carbohydrates] | Food[Fat] |
| Stomach[Carbohydrates] | Stomach[Fat] |
| Arterial[Carbohydrates] | Arterial[Fat] |
| Veneous[Carbohydrates] | Veneous[Fat] |
Dependent batches
Sometimes the possible independent sets of states are too few, or the number of states in each is too large.
Dependent batches mean that batches are created as sequences, where the results of each batch is stored so that it can be used as an input to the next batch. In the model above, the Food compartment is not dependent on the remaining three compartments. One could therefore first solve the system of equations for Food, save the results and use them as an input when solving the equations of Stomach, Veneous and Arterial.
There are several caveats to keep in mind when setting up dependent batches:
When states that in reality belong together are solved independently, the solver might be fooled to use inaccurate error tolerances.
Consider the example above:
The transfer from Food to Stomach is a simple linear relationship: an amount proportional to the current amount in Food is taken from Food and put into Stomach. This type of model is (often) very easy for the solver, which will result in large time steps. However, if the processes in the remaining model are very sensitive to the amount received from Food, the solver will take small time steps. If these are run in different batches, the resolution of the input data might be too poor to give good results for the remaining model.
The amount of data to store for each batch can become very big
When the amount of data is big, it takes a long time to look up input data. It is therefore not certain that a batch simulation will run faster than a normal simulation.
This being said, dependent batches are sometimes the only possibility to run really large models. A typical situation when dependent batches are useful is when a model consists of a chain of sub-models.
See also
- Batch simulation settings
